THE SINUSOIDAL WAVE
The simplest vibratory motion is the sinusoidal one. The most comprehensible sinusoidal oscillator model, in addition to the plate mentioned in the previous chapter, is the simple pendulum. It consists of a fixed support with a not elastic cord to which a mass is hung. When, with a hand movement, we slightly move the weight at one side, thus giving energy to the pendulum, we notice that it falls again due to the force of gravity with increasing speed up to a maximum localizable in the rest point. Subsequently it dispatched the reached energy reascending on the opposite side with decreasing speed until stopping for a moment and then felling and climbing again so completing a cycle. Cycles will continue with increasingly less wide oscillations up to exhausting, because of friction, all the energy transmitted by the hand movement. By exploring closely these pendulum motions we realise that the pendulum oscillations are isochronous, that is, independent of the size of the oscillations, the complete round trip (called period) is always the same.
These pendulum characteristics are also found in sinusoidal waves.
The figure charts show all these features. Figure 5 shows the pendulum in its rest position (in relief with a wider trait) and simultaneously in the extreme swinging points to the left and to the right. It is a representation of overlapping pictures at a time distance.
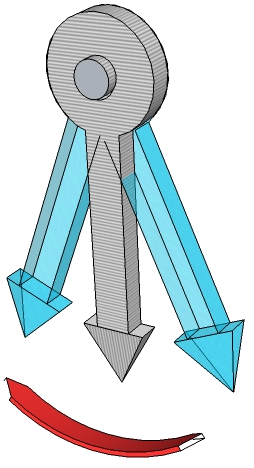
Figure 5
Figure 6 shows the pendulum oscillations in the various moments (represented on different boxes) of six whole periods. Note that the movement tends to have smaller oscillation amplitude.
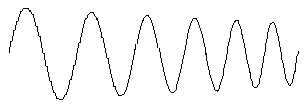 |
 |
| Figure 6 | Figure 6 for embossed printing |
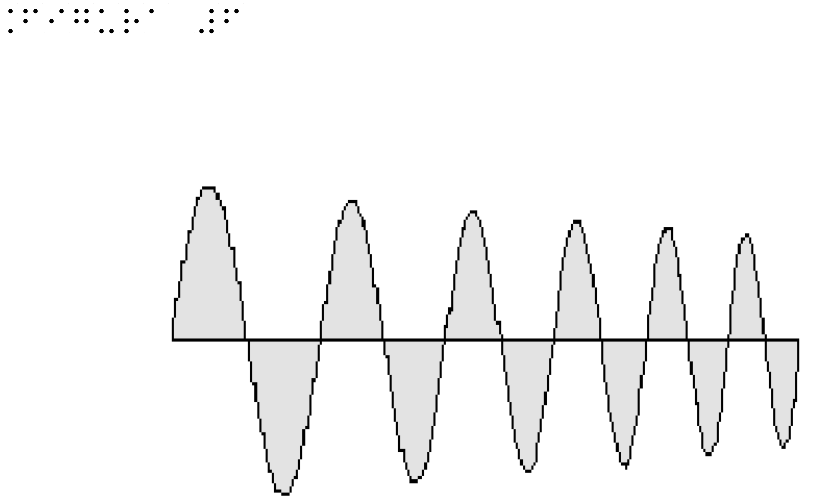
Figure 7 shows the chart of a sinusoidal wave indicating on the ordinate axis the amplitude of the wave and the abscissa axis the time.
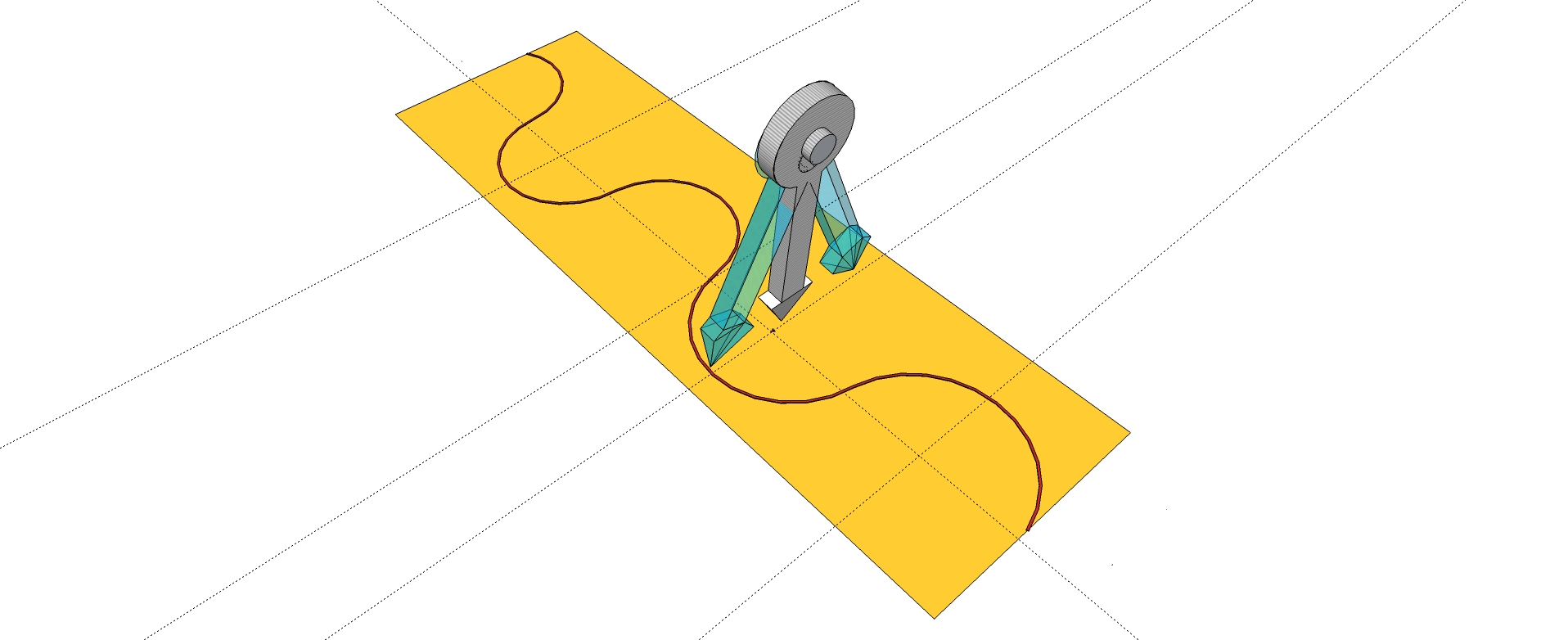
Figure 7
Finally, Figure 8 shows a sinusoidal wave in space as a succession of compression and rarefaction moments.
 |
 |
| Figure 8 | Figure 8 for embossed printing |
It is interesting to note the practicality of a representation on Cartesian axes (amplitude on time) since we can quickly find the amplitude related to passed time. Do not confuse, however, this chart with the drawing of the trajectory of many points or as the real path of a point, but simply consider it as a practical representation of an oscillation. A theoretical way to obtain a similar chart, as that of the above Figure 7, is that to equip the lower part of the pendulum with a nib so that it can draw the chart on a roll of paper that runs at a constant speed.
